Photo Credit: koya979 / Shutterstock.com

Crystal Physics

G4CMP comes with configuration data for germanium and silicon crystals in the package itself using the G4LogicalLattice and G4PhysicalLattice classes. G4CMP provides a collection of physics processes for simulating interactions in these types of crystal lattices. A list of things crystal interactions that G4CMP models: Acoustic phonons, electrons, holes in cryogenic crystals, anisotropic phonon propagation, oblique carrier propagation and phonon emission by accelerated carriers. The following serves as a summary of the physics G4CMP utilizes.

Crystal Lattices

G4CMP comes with configuration data for germanium and silicon crystals in the package itself using the G4LogicalLattice and G4PhysicalLattice classes; these are found in the CrystalMaps directory, where users can also define crystals of other materials. These config.txt files are plain text with names, values, and units. User applications must specify the config name separately from the G4Material name. Each lattice definition requires several sections:

Crystal parameters
Phonon parameters
Charge carrier parameters
Hole and electron masses

The material properties and crystal structure are implemented via the G4LogicalLattice class, which provides the natural coordinate frame of the lattice and associates it to a specific Geant4 “placement volume” with an orientation. The G4PhysicalLattice class handles local/lattice/valley coordinate transforms.

Charge Transport

Physically, charge transport occurs when incident particles promote electrons to the conduction band, simultaneously creating holes. However, there are several peculiarities of charge transport that G4CMP simulates which are worthy of note.

Valleys and Intervalley Scattering

The lowest energy bands in crystals have particular orientations, called valleys. Electrons travel along valleys but are also scattered between them. Electrons are transported along valleys because they have different effective masses parallel and perpendicular to the valley axis—this means that they might have different masses in multiple directions. This is modeled by the Electron Mass Tensor. In particular, letting the valley axis be x, ${"id":"1","font":{"size":11,"color":"#000000","family":"Arial"},"code":"$$m̳\\,=\\,\\begin{bmatrix}\n{m_{\\parallel}}&{0}&{0}\\\\\n{0}&{m_{\\perp}}&{0}\\\\\n{0}&{0}&{m_{\\perp}}\\\\\n\\end{bmatrix},\\,\\vec{p}\\,=\\,m̳\\,\\vec{v},\\,E\\,=\\,\\vec{p}^{T}m̳^{-1}\\vec{p}$$","aid":null,"backgroundColorModified":null,"type":"$$","backgroundColor":"#ffffff","ts":1657901544486,"cs":"KWO6baaubdGb7rh2qCnpFQ==","size":{"width":384,"height":66}}$

This relationship only applies close to the valley axis, and in general the Mass tensor is direction-dependent. G4CMP uses a fixed mass tensor for all kinematics.

Intervalley scattering occurs when electrons are strongly scattered by absorption of thermal phonons—a large momentum transfer can move an electron from one valley to another. This scattering contributes to electron drift speed.

G4CMP models this process with the G4CMPInterValleyScattering class, with several options for determining the scattering rate. For that purpose, the user may use G4CMPIVRateLiner, G4CMPIVRateQuadratic, or G4CMPInterValleyRate.

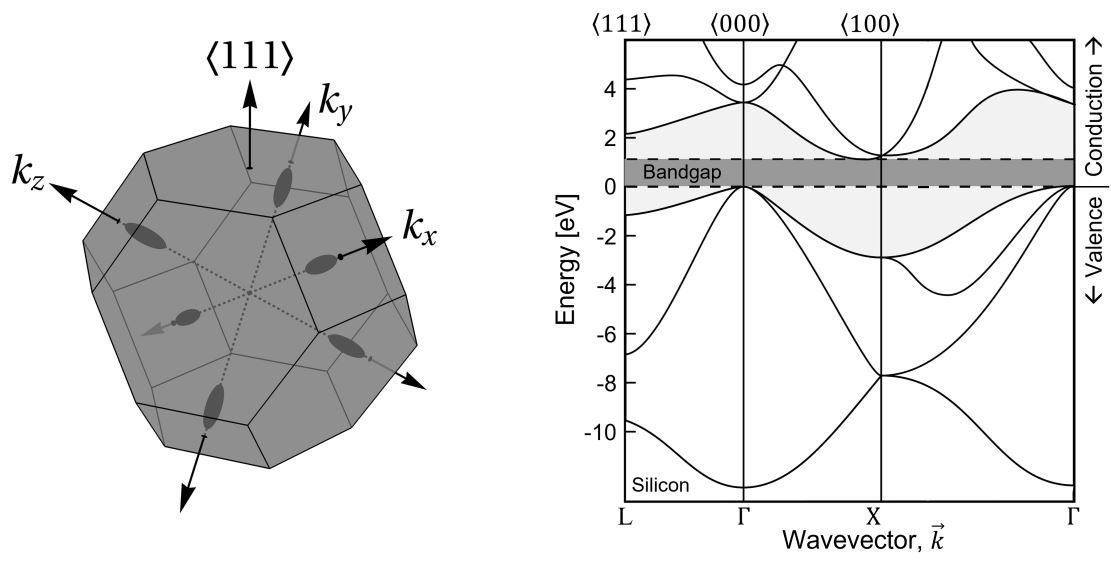
Left: The first Brillouin zone for Si, reproduced from Ref. [49]. The minimum-energy valleys of the conduction band are indicated by the ellipsoids near the edge of the Brillouin zone along the kx, ky, and kz directions. Right: Energy band structure for Si (adapted from Ref. [50]), highlighting the bandgap between the valence-band maximum along the <000> direction and the conduction-band minimum along the <100> direction. The latter corresponds to the minimum-energy X valleys (ellipsoids in the left panel). Similar diagrams can be found in Ref. [51] for Ge, which has its conduction-band minimum along the <111> direction (L valleys).

Phonon Emission

Charges accelerated in an electric field can radiate phonons. These Phonons are known as Neganov-Trofimov-Luke (NTL) Phonons, and are emitted when charges accelerated by an E-field attain velocities well above v_sound. This occurs when the charges interact with the lattice, radiating phonons, reducing their energy, and changing direction. The phonon emission rate can be modeled by,

${"code":"$$\\nu=\\frac{3l_{0}}{v_{sound}}\\frac{Ma}{\\left(Ma-1\\right)^{3}}$$","backgroundColor":"#ffffff","backgroundColorModified":null,"aid":null,"type":"$$","id":"3","font":{"family":"Arial","size":11,"color":"#000000"},"ts":1657902222106,"cs":"YjYy9O8zzLihbXcjnlf2nA==","size":{"width":162,"height":42}}$

With total phonon emission equalling energy gained from the potential difference across which the charge accelerates. Here, l0 is the scattering length for the charge type and Ma is the Mach number (v/vsound) for the charge.

The class G4CMPLukeScattering implements this phenomenon, with rate determined by the G4CMPLukeEmissionRate class.

Charge Recombination

One “fact of life” in the Geant4 framework is that particles are independent and isolated—they do not mutually interact. However, in the low-energy case, charges (i.e. electrons and hotels) at the surfaces of a crystal cannot escape because they do not “reflect” against the bias voltage. As a solution, G4CMP assumes that these charges recombine with some pre-existing partner (an electron with a hole or a hole with an electron).

When this occurs, half of the bandgap energy is released as phonons at the material’s Debye frequency.

Silicon: 15THz, 62.03 meV
Germanium: 2THz, 8.27 meV

Since electron-hole pairs are created initially, both charges recombining and releasing half the bandgap energy ensures energy conservation.

This process is modeled in G4CMP in the G4CMPDriftRecombinationProcess class.

Charge Trapping on Impurities

Similarly to recombination, this occurs when charges become stuck in place. Trapping, however, occurs when charges are stopped by impurities in the bulk of the detector material. When particles are trapped at a shallow (~ meV) depth, the bandgap energy is not recovered.

There are two types of impurities in the crystal lattice, resulting in four kinds of capture, one for each kind of charge and impurity:

e + D0 → D—, e + A+→ A0, h + A0 → A+, h + D—→ D0

These captures have separate rates for electrons and holes. They can also be device-dependent and even history (neutralization) dependent.

Charges trapped in this way can contribute to the detector’s charge collection signal if they are trapped near enough to the electrodes.

This process is modeled with the G4CMPDriftTrappingProcess class, with the electron and hole trapping lengths managed by the corresponding configuration commands:

/g4cmp/electronTrappingLength 
/g4cmp/holeTrappingLength

These parameters are global for an entire computing job; that is, G4CMP assumes that the user is simulating a single device. Versions of these parameters that are attachable to individual detector volumes may be implemented in the future.

Impurity Trap Reionization

Trap Reionization is essentially the inverse of trapping. Tracks can interact with traps that have immobilized a charge, releasing charges. When this occurs at a shallow (~meV) depth, the bandgap energy is not absorbed.

Two types of impurities here result in four types of reionization each with a separate rate.

e + D− → 2 e + D0 , e + A+ → e + h + A0
h + A0 → 2 h + A+ , h + D− → h + e + D0

As before, rates can depend both on device and neutralization history.

The G4CMPDriftTrapIonization class handles this process in the package, and has corresponding configuration commands.

/g4cmp/eDTrapIonizationMFP 
/g4cmp/eATrapIonizationMFP 
/g4cmp/hDTrapIonizationMFP
/g4cmp/hATrapIonizationMFP

As in the previous section, these are global parameters.

Phonons

Phonons are a type of energy-carrying quasiparticle; in particular, they consist of quantized lattice oscillations that occur in several ways. Phonons can either be longitudinal (compression waves), or transverse (shear waves), and can propagate in either low energy (“acoustic”) or high energy (“optical”) states.

Phonon Mode Group Velocity

Using the crystal stiffness matrix along a given , we have the Christoffel matrix , whose eigenmodes are phase velocity and polarization. Group velocity is then computed from these factors. In order to speed up processing, G4CMP generates lookup tables with steps of coordinates and interpolates between steps. These processes are governed by the G4CMPPhononKinematics class.

Phonon Impurity Scattering and Anharmonic Decay

Phonons can scatter off of impurities in the crystal lattice, changing their mode, from longitudinal to slow or fast transverse, for example. The rate of this scattering scales like E4. Specifically, =, where B = 2.43×10-42s3 in Silicon.

G4CMP implements this phenomenon using wavevector (energy) conservation. A different mode is chosen based on the configured density of states, and uses the corresponding wavevector to determine the phonon’s new velocity vector. This is governed by G4PhononScattering and supplemented by G4CMPPhononScatteringRate.

Another possibility after scattering, besides transforming modes, is splitting into pairs of various modes. Longitudinal (L) phonons can do this, splitting either into two transverse (T) phonons or a new longitudinal (L’) and transverse (T) phonon. The rate of this process scales like E5. In particular, , where D = 2.43×10-42s3 and the fraction of decays to TT compared to L’T pairs is 0.74 in Silicon. The splitting process equipartitions early “hot” (Debye energy in the tens of meV) phonons into a sea of meV-scale phonons. G4CMP uses G4PhononDownConversion and G4CMPDowncoversionRate classes to manage the simulation of this process. After early high-energy phonons split in the wake of an energy deposit, the detector crystal becomes filled with a “gas” of low-energy (≲ meV) phonons with all modes represented, moving in all directions. Sensors on the top and bottom of the crystal can absorb phonons to measure the magnitude of the energy deposit.

Comparison of phonon caustics predicted for a point source in a 1 cm thick Ge <100> crystal with corresponding results from G4CMP, showing positions
of transverse phonon modes on the face opposite the point source. Left: Outline of phonon caustics in Ge <100> as predicted by Nothrop and Wolfe [34]. Middle: Caustics pattern as simulated using G4CMP for phonon transport in Ge <100>, in good agreement with the theoretical prediction to the left. Right: Caustics pattern as simulated using G4CMP for phonon transport in a 1 cm thick Si <100> crystal

Energy Partitioning in G4CMP

Geant4 typically doesn’t produce “trackable” electrons below tens of eV. Instead, it records an “energy deposit” value associated with the electron’s parent track. In this method, dE/dx summarizes all the conduction electrons produced by a track. However, in semiconducting crystals, the minimum energy required to generate one electron-hole pair is the bandgap, at around 1 eV. In the end, the typical pair energy is 3-4 eV per pair, with some variation. Further, ions (including alpha particles) induce motion in nearby atoms in the lattice. This results in Non-ionizing energy loss (NIEL) and athermal phonons, each with a Debye energy in the tens of meV. G4CMP addresses these issues via the G4CMPSecondaryProduction and G4CMPEnergyPartition classes, allowing for charge tracking at the lower energy levels used in low-temperature measurement that is otherwise impossible in Geant4. The Relative magnitude of dE/dx versus NIEL for ions depends on the charge and mass of the projectile as well as atomic number and mass of the crystal atoms. The ionization yield is computed by taking dE/dx as a fraction of the total. G4CMP does this in its code for ion hits, but it is now done automatically in Geant4 10.7: the issue is addressed via forward-compatibility, because G4CMP will not recalculate the yield in the case of non-zero NIEL. This process remains in the G4CMPLindhardNIEL and G4CMPLewinSmithNIEL classes.